Exercise 1.19: Two-bar linkage

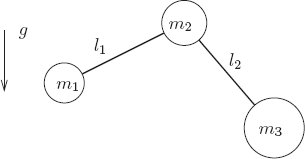
The two-bar linkage shown in the figure below is constrained to move in the plane. It is composed of three small massive bodies interconnected by two massless rigid rods in a uniform gravitational field with vertical acceleration g. The rods are pinned to the central body by a hinge that allows the linkage to fold. The system is arranged so that the hinge is completely free: the members can go through all configurations without collision. Formulate a Lagrangian that describes the system and find the Lagrange equations of motion. Use the computer to do this, because the equations are rather big.

Figure 1.3

Figure 1.3

Use three sets of rectangular coordinates, one for each body. The generalized coordinates could be represented by the position of $m_2$ and two angles, $\theta_1$ and $\theta_3$, positive CCW and measured from the X axis.

$$ \begin{align*} x_1(t) &= x + l_1\cos\theta_1 \\ x_1(t) &= y + l_1\sin\theta_1 \\ x_2(t) &= x\\ y_2(t) &= y\\ x_3(t) &= x + l_1\cos\theta_3 \\ x_3(t) &= y + l_1\sin\theta_3 \\ \end{align*} $$

(defn twobar-linkage->rect [l_1 l_2]
    (fn [[_ [x y theta_1 theta_3] _]]
        (up (+ x (* l_1 (cos theta_1)))
            (+ y (* l_1 (sin theta_1)))
            x
            y
            (+ x (* l_2 (cos theta_3)))
            (+ y (* l_2 (sin theta_3)))
        )))

(defn L-const-accel-three-bodies [m_1 m_2 m_3 g]
    (fn [[_  [x_1 y_1 x_2 y_2 x_3 y_3] [v_x1 v_y1 v_x2 v_y2 v_x3 v_y3]]]
        (let [T1 (* 1/2 (* m_1 (+ (square v_x1) (square v_y1))))
              T2 (* 1/2 (* m_2 (+ (square v_x2) (square v_y2))))
              T3 (* 1/2 (* m_3 (+ (square v_x3) (square v_y3))))
              T (+ T1 T2 T3)
              V1 (* m_1 g y_1)
              V2 (* m_2 g y_2)
              V3 (* m_3 g y_3)
              V (+ V1 V2 V3)]
        (- T V))))
           

(defn L-twobar-linkage [m_1 m_2 m_3 g l_1 l_2]
    (fn [q-prime]
          ((compose (L-const-accel-three-bodies m_1 m_2 m_3 g) (F->C (twobar-linkage->rect l_1 l_2)))
           q-prime)))

(def eom-twobar-linkage  
 (let [L (L-twobar-linkage 'm_1 'm_2 'm_3 'g 'l_1 'l_2)]
    (Lagrange-equations L)
))

(rendertexvec
 (let [state (up (literal-function 'x) (literal-function 'y) (literal-function 'theta_1) (literal-function 'theta_3))]
     ((eom-twobar-linkage state) 't)))

\begin{pmatrix}\displaystyle{- l_1\,m_1\,\cos\left({\theta}_1\left(t\right)\right)\,{\left(D{\theta}_1\left(t\right)\right)}^{2} - l_2\,m_3\,\cos\left({\theta}_3\left(t\right)\right)\,{\left(D{\theta}_3\left(t\right)\right)}^{2} - l_1\,m_1\,\sin\left({\theta}_1\left(t\right)\right)\,{D}^{2}{\theta}_1\left(t\right) - l_2\,m_3\,\sin\left({\theta}_3\left(t\right)\right)\,{D}^{2}{\theta}_3\left(t\right) + m_1\,{D}^{2}x\left(t\right) + m_2\,{D}^{2}x\left(t\right) + m_3\,{D}^{2}x\left(t\right)} \cr \cr \displaystyle{- l_1\,m_1\,{\left(D{\theta}_1\left(t\right)\right)}^{2}\,\sin\left({\theta}_1\left(t\right)\right) - l_2\,m_3\,{\left(D{\theta}_3\left(t\right)\right)}^{2}\,\sin\left({\theta}_3\left(t\right)\right) + l_1\,m_1\,\cos\left({\theta}_1\left(t\right)\right)\,{D}^{2}{\theta}_1\left(t\right) + l_2\,m_3\,\cos\left({\theta}_3\left(t\right)\right)\,{D}^{2}{\theta}_3\left(t\right) + g\,m_1 + g\,m_2 + g\,m_3 + m_1\,{D}^{2}y\left(t\right) + m_2\,{D}^{2}y\left(t\right) + m_3\,{D}^{2}y\left(t\right)} \cr \cr \displaystyle{g\,l_1\,m_1\,\cos\left({\theta}_1\left(t\right)\right) + {l_1}^{2}\,m_1\,{D}^{2}{\theta}_1\left(t\right) + l_1\,m_1\,\cos\left({\theta}_1\left(t\right)\right)\,{D}^{2}y\left(t\right) - l_1\,m_1\,\sin\left({\theta}_1\left(t\right)\right)\,{D}^{2}x\left(t\right)} \cr \cr \displaystyle{g\,l_2\,m_3\,\cos\left({\theta}_3\left(t\right)\right) + {l_2}^{2}\,m_3\,{D}^{2}{\theta}_3\left(t\right) + l_2\,m_3\,\cos\left({\theta}_3\left(t\right)\right)\,{D}^{2}y\left(t\right) - l_2\,m_3\,\sin\left({\theta}_3\left(t\right)\right)\,{D}^{2}x\left(t\right)}\end{pmatrix}